Posted by

Posted on

November 27, 2025

Posted under

Comments

A simple explanation of the big idea behind public key cryptography

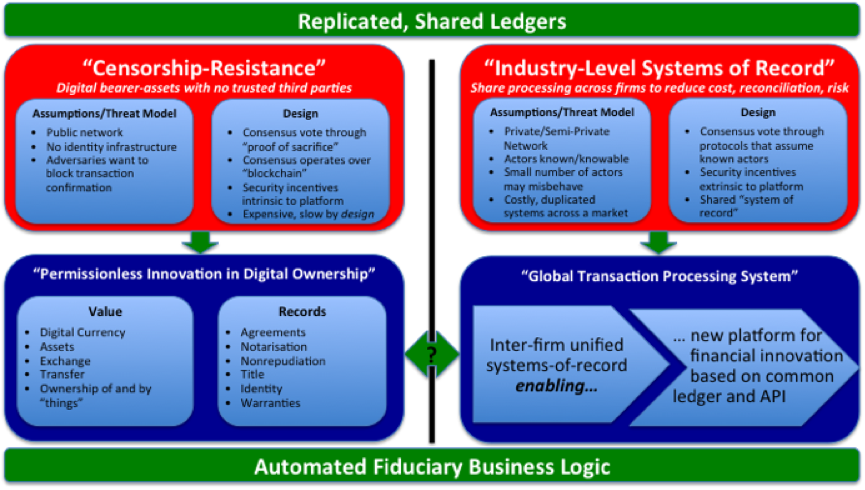
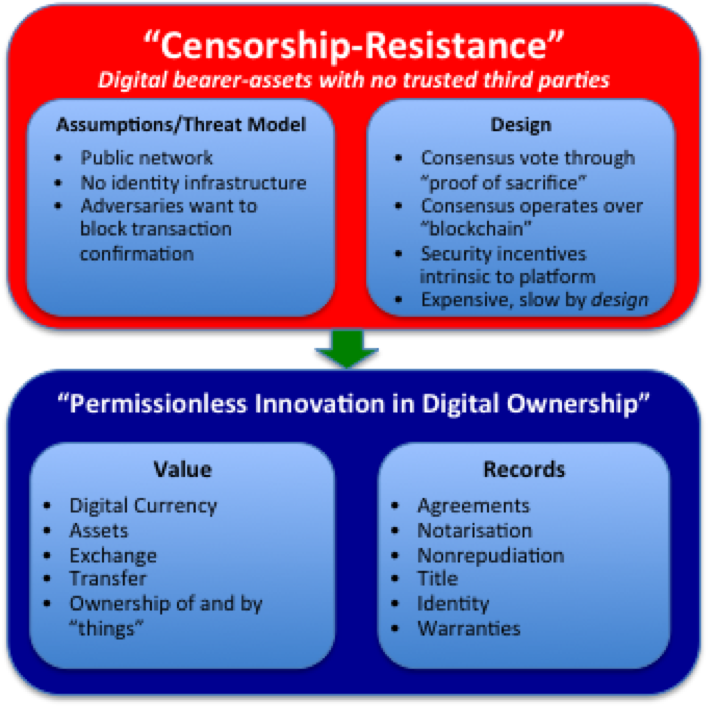
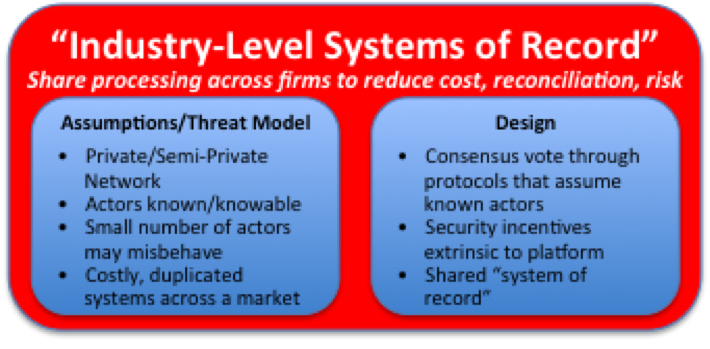
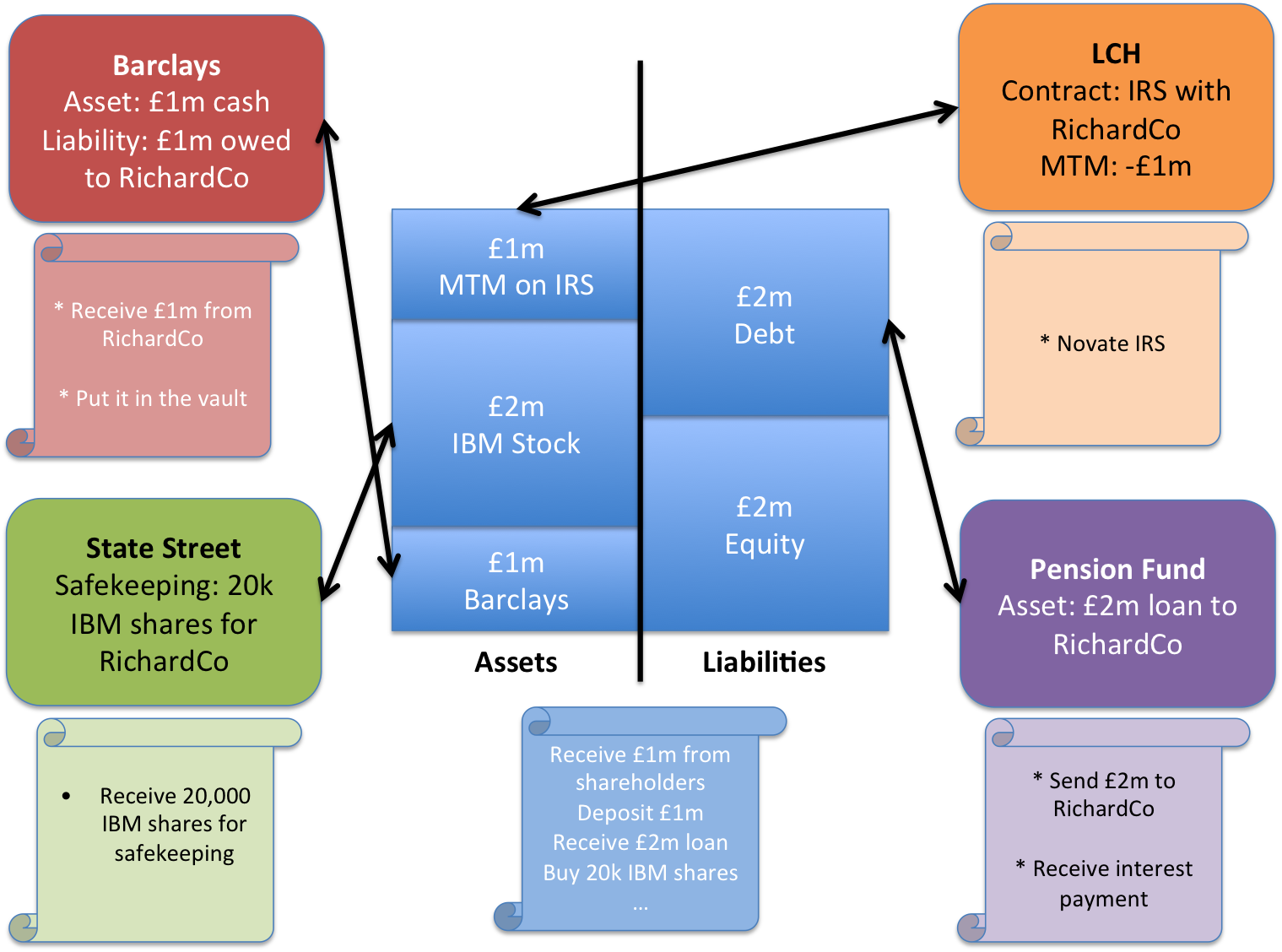
Have you ever read a non-technical article about public and private keys, but found it all just a bit too vague and unsatisfying? If so, this piece is for you…

Nic Carter published a good piece the other week on how Bitcoin’s security works, in the context of quantum computing. It’s not easy to explain this stuff and I thought he did a really good job.

He talks about digital signatures, and how difficult it is to impart intuition for how they work. I think this is because it’s really hard to explain how public key cryptography works. And if a reader has no mental model for the latter then they’re never going to develop intuition for the former.

How to explain the big idea behind public and private keys?

This piece might look long at first – but don’t be put off. It’s really just a super simple sequence of steps… something that a child with a basic understanding of multiplication could understand. Yet, by the end, you’ll have learned how to convince somebody you know a secret without them having any clue whatsoever what that secret is. And this trick – convincing somebody of something without showing it to them – is at the heart of public key cryptography.

So here goes…

How do you keep secrets when everything is public?

A fundamental problem that blockchain systems have is that everything happens in public… everything is potentially visible to everybody else. So how do you keep things secure? How do you prove you own a token when you want to spend it, without revealing your ‘password’ to everybody else?

This problem is directly analogous to the one faced by the Forty Thieves in the famous Arabian folk tale: how to secure their cave?

Their solution was reasonable enough at first: a secret phrase. Anybody who knew this phrase, literally a password – ‘Open Sesame!’ – merely had to shout it at the entrance and the stone securing the cave would roll away. Simple, and effective. At least for a while.

The problem, just like ours, was eavesdroppers.

The act of using a password also reveals the password to anybody nearby who might be listening.

Ali Baba was one such eavesdropper. He overheard the thieves one day and learned the password. He was then able to gain access to the cave, and to explore the riches within.

So our challenge is: can we come up with a way to prove you know a password without actually saying it out loud?

What could the thieves have done to make their system more secure?

Don’t be downhearted if you can’t figure out an answer: nobody else knew how to solve it until a few decades ago. But transactions on public blockchains remain safe only because it has been solved.

A simple number game that is surprisingly profound

To get us started with a potential solution I want you to temporarily pretend to believe something that sounds obviously untrue. I want you to imagine that nobody in the world – nobody whatsoever – knows how to factorise numbers.

Imagine you are presented with the number 6. I need you to believe that nobody could figure out that it is 2 x 3.

Similarly, somebody might give you the number 15 and you’ll have no concept that it is 3 x 5. You see 15, but which smaller numbers it may be made up of is just a complete mystery to you. You would consider it absurd even to try to figure out the answer.

Here’s a game you could play with a friend, Alice, in a world where nobody can factorise numbers.

First, pick two numbers at random, in secret. Perhaps you pick 3 and 5. Keep them to yourself for now.

Now you take your numbers – 3 and 5 – and multiply them together, getting 15.

At this point, you know 3 and 5, and you know they multiply together to get 15.

Share one of your smaller numbers – let’s say 5 – with Alice, along with the bigger number, 15.

So, you know 3, 5, 15. And Alice knows just 5 and 15.

You say to Alice:

“Here is a number: 15. One of the factors is 5. I also know the other factor. I’m going to prove that I know this to you. When this game is over, you will fully believe that I know the other factor, but you will have no idea what it is, and neither will anybody else.”

Proving you know something without revealing it

Here’s how you could prove to Alice that you really do know how to factorise 15 without ever revealing that one of the factors is 3.

The trick is that you ask Alice to think of another random number, that she will keep secret from you.

Let’s say Alice picks 13 as her secret number.

Ask her to do two things:

First she multiplies her secret number – 13 – by the number she can’t factorise – 15 – to get 195, which she also keeps to herself.

Second, she multiplies the secret number – 13 – by the factor of 15 she does know – 5 – to get 65.

So, she knows 13 x 5 (65) and she knows 13 x 15 (195). She doesn’t know the other factor of 15 (3), of course, but she is aware of something important: she knows that if 65 were multiplied by the secret factor – whatever it is – the answer will be 195.

She knows this because multiplying by a number is the same as multiplying by all its factors. For example, multiplying by 6 is the same as multiplying by 2 and then multiplying the result by 3.

So, even though she doesn’t know your other secret factor she knows that if you multiply 65 by your secret factor – whatever it is – you’re guaranteed to get 195.

To emphasise: she knows this because 195 is 13 x 15, which must also be the same as 13 x 5 multiplied by the secret factor.

But only somebody who had knowledge of that secret factor – you – could do this.

She now shares the number 65 with you, which she alone knows is 13 x 5. You, of course, have no idea how to factorise this number so you don’t know that 65 is 13 x 5. All you see is 65.

Alice now challenges you to multiply 65 by the secret factor.

So you perform the calculation:

65 x 3 = 195.

Recall that the only person who could independently perform this step of the calculation is somebody who knows the secret factor: you.

After sharing your answer – 195 – with Alice, she checks this against her own calculation (13 x 15), and sees that you have both calculated 195.

But the only number she had shared with you was 65, which only she knows is 13 x 5.

She therefore concludes that you must definitely know the other secret factor to 15, because it was only by multiplying 65 by the secret factor that you could possibly have figured out the answer to her challenge.

You have proved that you know the secret factor to her without revealing it to her.

And here’s another cool thing: the next time somebody comes along, she can pick a different random number… maybe 23. She’d calculate 23 x 15 = 345, and 23 x 5 = 115, and share the 115. The only way the next person could perform the right calculation (115 x 3 = 345) is if they knew the secret factor, 3.

An attacker who had eavesdropped on the previous conversation would have learned nothing of any use in answering the new challenge.

Isn’t that amazing? We’ve figured out a way to prove to somebody that you know a secret password without anybody, not an eavesdropper and not even the person you’re proving it to, learning what it is!

The idea underpinning this example – that if factorisation is impossible or very difficult then you can prove you know things without revealing them – sounds absurd. But it turns out there are many mathematical systems where operations akin to factorisation are indeed extremely hard. In other words, my ludicrous assumption – that factorising numbers is hard – isn’t actually all that ludicrous in the context of the mathematical systems used by modern cryptographers.

Of course, real cryptographic systems work differently to this, but not by as much as you might think… if you can assume an operation such as factorisation of numbers is difficult, you can build a system that lets you use a password without ever revealing what it is.

We call such systems public key cryptography systems, and they’re the basis of how systems like Bitcoin – and other blockchains – stay secure, even though everything happens completely in public.

This trick — proving you know a secret without revealing it — is the heart of modern blockchain security. It’s why users can transact in full public view without ever exposing the keys that control their assets. And it’s precisely this cryptographic foundation that allows institutions, such as those I’m bringing to Solana in my role as CEO of R3 Labs, to issue and trade real-world assets on public networks with confidence.

The solution that finally solved the Forty Thieves’ problem mere decades ago now gives institutions the confidence they need to issue billions of dollars of value on public chains. What a remarkable story.

Posted by

gendal

Posted on

August 17, 2015

Posted under

Bitcoin, bitcoin xt, block size, governance

Comments

148 Comments

Brief thoughts on the Bitcoin block size debate

I’ve kept well away from the block size debate but the launch of Bitcoin XT is worth a quick mention.

My reasons for staying out of the debate are pretty obvious: I’m not a miner, I’m not a core developer, I don’t run a wallet service, I have no particular insight into the engineering trade-offs and, perhaps most importantly, I’m not mad. If I wanted to argue with people on the internet, there are far more interesting topics than Bitcoin’s block size…

But I’ve been asked by several people what I think. And, at core, I think it might come down to three issues: 1) fear of two different types of failure, 2) a clash of visions and 3) no process for reconciling the first two issues.

Fear of Two Different Types of Failure

Fear of technical failure

I don’t contribute, but I do read the Bitcoin Development mailing list. I find it immensely helpful in keeping up with much of the day-to-debate debate. What becomes clear when you read it is that there are (at least!) two distinct cultures at work.

First, there is a very strong security engineering culture. I sometimes think the trick to being a good security engineer is to think like a software tester (and vice versa): “How could I break this?”… “How could an attacker get round this?”… “What could go wrong here?”… “How could I force the provider of this service to waste all their resources” And so on. Your job is to figure out all the ways something could fail, and fix it.

So, when presented with something like an increased block size, you obviously focus on all the things that could go wrong: miners on slow connections could get out-of-sync with those on the other side, the increased cost of running a node could create a centralisation pressure and so on. And when you compare this against the potential benefits, you might not think the change makes sense: there’s an increased technical and security risk but you haven’t fixed the underlying scalability issue at the heart of the system… you have, in some ways, just kicked the can down the road. So you might say that a driving issue here is “fear of technical failure”: the change, which has uncertain benefits, could cause catastrophic harm. Better not do it just yet.

Fear of practical failure

But, on the other side, is a somewhat different culture, one that comes from a world where there are problems everywhere you look and they all need fixing. So you pick the biggest one, fix it and move on. The engineering functions of large companies are often like this. You know your change might cause problems but if you believe “doing nothing” is not an option then it comes down to making the least-worst decision. There are, after all, usually no good solutions, just compromises.

So, if you’re faced with a problem like blocks getting full in some foreseeable timeframe, it is natural to ask yourself: what is the risk of doing nothing? If your belief is that consumers mostly have choices and will simply abandon a system that can’t guarantee transaction confirmation in a reasonable period then you’ll likely see failure to increase the block size as something that will lead to a catastrophic exodus of users and your bias will likely be towards making the change. For you, the issue is “fear of practical failure”: failing to increase the blocksize, a change which has uncertain risks in any case, will drive away users and make the system a failure in all practical cases.

I exaggerate for effect, of course and I’ve ignored many aspects of the argument (e.g. the fee market, etc). And I’m sure some of the details are simply wrong. But note: even under this simplistic model, it doesn’t mean either side is “wrong” or “bad”: it is possible to hold either view quite legitimately and to passionately believe the other side is wrong

A Clash of Visions

Where it gets more complex is when it comes to vision: if there was common agreement on what outcome was desired (e.g. “x transactions per second across the blockchain by 2017” or “the system should support this number of consumer wallets”) then the discussion would be a pure engineering discussion: “what is the best way to achieve this goal?” But it strikes me that there isn’t agreement on this underlying vision.

And so, the engineering discussions get lost in the sound of people talking past each other or, worse, resorting to ad hominem arguments. If you’re arguing from different premises, you never get anywhere, sadly. It’s what makes political discussions on the internet so tedious..!

Process

In most projects, these issues can be resolved, ultimately, through the “benevolent dictator” model. Linus just decides. Unfortunately, that process just doesn’t work in a system like Bitcoin. It’s not enough to control which code goes into the “core” distribution: the prevailing network rules are a complex function of miner adoption, full node adoption, wallet adoption, major merchant/processor adoption, and more. It’s an inherently messy and political process. So the block size debate is likely to just be the first of many such controversies in this world. The launch of Bitcoin XT is an interesting way to force the debate towards a conclusion but it’s likely to be messy.

And I hope those looking at “private blockchains” aren’t feeling smug as they read this. Managing the maintenance and upgrades of shared ledger systems between firms won’t be a walk in the park, either.

I have no particular insight into where this will go or which vision of the future will prevail. But I hope (perhaps forlornly) that it will be resolved through the actions of professionals acting in good faith and that neither side will resort to “dirty tricks”.

Posted by

gendal

Posted on

July 23, 2015

Posted under

Bitcoin, blockchain, ledgers, models

Comments

47 Comments

Bitcoin and Blockchain: two revolutions for the price of one?

I gave a brief talk on Bitcoin and blockchain technology to an audience of non-specialists at a dinner last week. It covers many of the themes I’ve explored on this blog before. But the short, fifteen-minute, format forced me to be brief and clear. This is an edited version of the speech

A £20 note has an obvious, yet extraordinary super-power. I can hand it to anybody in this room and £20 of value will be transferred instantly, directly, peer-to-peer, person-to-person. Settlement, with finality, in central bank money! And nobody else need know. And nobody can stop me.

Super £20!! [I really hope there’s no law against posting photos of money…]

But this super-power only works at close distance. If I want to transfer £20 of value to somebody in a different town or in a different country, I need to trust other people. Sure: I could put the £20 in an envelope and post it. But even then I’d have to trust the postal service.

Or I could use a bank. But I’d be trusting them to be good for the money. And I’d have handed over control: if my name’s on the wrong list, the bank would be obligated to seize my funds. And if you’re on the wrong list, the bank will refuse to transfer the money to you…

“Digital” money is not the same as physical cash.

And the world’s financial plumbing – payments systems, correspondent banking, SWIFT, … – is a direct consequence of this observation: physical cash really is fundamentally different to every other form of money: only physical cash is a bearer instrument. And only physical cash can be transferred without permission – censorship-resistant.

Or so we thought.

Because a curious email to an obscure cryptography mailing list at the end of 2008 said something quite audacious. The email, from the hitherto unknown Satoshi Nakamoto heralded the arrival of Bitcoin and the advent of “purely peer-to-peer electronic cash”.

“A purely peer-to-peer version of electronic cash”

We all know the story of what happened next.

Except… what many people have missed is that the choice of the word “cash” in that email was absolutely critical and absolutely deliberate. What this email announced was the arrival of a digital bearer asset that is censorship resistant. Digital cash. A digital asset that you can hold outright, with no risk of confiscation, and which you can transfer to anybody you choose with no permission from anybody else.

And the funny thing is: the architecture of Bitcoin flows almost trivially (almost…!) from this requirement. Proof-of-work, the peer-to-peer gossip network, mining, the mining reward, the blockchain. The lot. It’s as if the genius of bitcoin was to ask the question.

But why am I saying this in the summer of 2015? This exact same thing could have been said at any point from 2009 until now. There’s nothing new here.

Except…

Nobody asks the obvious question:

Who actually wants a censorship resistant digital bearer asset?!

Well… some people do, of course. But none of them are banks or corporates. At least, I’ve not yet met a bank that wants this.

So why are so many banks, corporates, VCs and startups spending so much money in this space?!

I think there are two completely distinct reasons and that that the world of “blockchain technology” is actually two completely different worlds, with different opportunities and different likely winners. And those who don’t realise this might be about to lose a great deal of money.

First, let’s look at Bitcoin.

We should probably be realistic here. Bitcoin is not the solution to Greece’s crisis and it won’t bring finance to the world’s poor. But it turns out that censorship resistance is extremely valuable, even for people who don’t think they need it.

Because censorship resistance implies openness.

Anybody or anything can connect to an open network like Bitcoin to own and transfer value. And anything that is open, standardised, owned by nobody and useful smells very much like a platform. And we’ve seen how those stories play out.

But notice something else: Bitcoin is worse than existing solutions for all the use-cases that banks care about. It’s expensive. It’s slow. And it’s “regulatorily difficult”. And this is by design.

So this makes it doubly interesting.

Because it means Bitcoin is probably worse than existing solutions for all the things most people and firms care about but vastly better for one single use-case (open access to value transfer) that could be very useful for some people.

Isn’t that pretty much the definition of a disruptive innovation? Something that’s worse for existing use-cases but solves a niche use-case very well?

So, if this is true, we should expect to see adoption of Bitcoin come from the margins, solving marginal problems for marginal users.

But disruptive innovations have a habit of learning fast and growing. They don’t stop at the margins and they work their way in and up.

So this is why I think so many of the big-name VCs are so excited about it.

So the incumbents should be keeping a very close eye on what’s going on. If anything in this space is going to disrupt them, it will probably come from this world. But it’s perfectly understandable that vanishingly few of them are actually engaging deeply in this world.

So if Bitcoin isn’t why banks are looking at this space, what are they looking at?

How have so many people convinced themselves that there is something of interest here that is “separate” to Bitcoin or systems like it?

At this point, it’s customary to observe sagely that “of course, the real genius of bitcoin was the blockchain; that’s where the value is”.

But I’ve discovered something rather amusing. If you push the people who say this, and ask them what they actually mean, most of them can’t! And yet… whether they understand why or not, they are actually on to something.

It comes down to how bitcoin delivers on the design goal of “censorship resistant” cash.

Imagine Bitcoin didn’t already exist and you were asked to design a system of censorship-resistant digital cash. How would you do i?

Well… you couldn’t build it around a central database: the government could shut it down. That doesn’t sound very censorship resistant.

And you couldn’t rely on a network of trusted people around the globe since law enforcement could simply collaborate to shut them down too. And in any case, who would control the identity system that helped you be sure these people were who you thought they were in any case?

It turns out that the answer is quite unexpected… and it’s something I’d bet almost all engineers would consider completely mad.

The answer is that you get everybody who fully participates in the system to maintain a full copy of the ledger. And every time somebody, anywhere in the world, spends some bitcoin, we’re going to inform everybody who’s maintaining this ledger and they’re going to store a copy of that transaction too.

Bitcoin essentially runs on a MASSIVELY replicated, shared ledger. (The trick is in keeping it consistent, of course…)

It sounds insanely inefficient and expensive… and perhaps it is. But we also have to ask ourselves: inefficient and expensive as compared to what?

And this leads us to the other world

Just look at the state of banking IT today… Payments, Securities, Derivatives… Pick any one. They all follow the same pattern: every bank has built or bought at least one, usually several, systems to track positions and manage the lifecycle of trades: core banking systems, securities settlement systems, multiple derivatives systems and so on.

Each of these systems cost money to build and each of them costs even more to maintain.

And each bank uses these systems to build and maintain its view of the world. And they have to be connected to each other and kept in sync, usually through reconciliation.

Take even the simplest OTC derivative contract: it is recorded by both sides of the deal and those two systems have to agree on everything for years. Very costly to operate.

But what if… what if these firms – that don’t quite trust each other –used a shared system to record and manage their positions? Now we’d only need one system for an entire industry… not one per firm. It would be more expensive and complicated to run than any given bank-specific systems but the industry-level cost and complexity would be at least an order of magnitude less. One might argue that this is why industry utilities have been so successful.

But a centralised utility also brings issues: who owns it? Who controls it How do the users ensure it stays responsive to their needs and remains cost-effective?

The tantalising prospect of the blockchain revolution is that perhaps it offers a third way: a system with the benefits of a centralised, shared infrastructure but without the centralised point of control: if the data and business logic is shared and replicated, no one firm can assert control, or so the argument goes.

Now, there are lots of unsolved problems: privacy, performance, scalability, does the technology actually work, might we be walking away from a redundant (antifragile?) existing model? Who will build these platforms if they can’t easily charge a fee because of their mutualised nature? Difficult questions.

But see: this has nothing to do with funny internet money, bitcoin or censorship-resistant digital cash. It’s a completely different world

Two revolutions for the price of one

So… the blockchain revolution is so fascinating because it could actually be TWO completely different revolutions… both profound in their implications:

Censorship-resistant digital cash providing a new platform for open, permissionless innovation driven from the margins
And industry-level systems of record driving efficiencies for incumbents.

Neither of these are “sure things”… they are both high risk speculative bets… but they’re also very DIFFERENT bets…

[EDIT 2015-07-23 Gideon Greenspan has written a great piece that comes at this argument from a very different angle]

As ever, the thoughts and comment on this blog are mine alone and don’t represent the view of my employer….

Posted by

gendal

Posted on

June 8, 2015

Posted under

Bitcoin, blockchain, replicated shared ledger

Comments

31 Comments

Towards a Unified Model for Replicated, Shared Ledgers

Don’t Say The “B Word”!

I’ve come to the conclusion that saying “blockchain” has become unhelpful. It just confuses people. It means too many different things to different people and so it’s almost impossible to have a conversation in this space without talking past each other. So, as I argued in this piece on permissionless ledgers and this piece on permissioned ledgers, it can be useful to talk in terms of replicated shared ledgers – since I think this gets to the heart of what unifies – and separates – these two worlds.

Shared: because multiple actors can read or write to different parts of the ledger
Replicated: because everybody who needs a copy can have a copy, rather than relying on a powerful central entity

In this piece, I try to bring it all together – to explain why we should be thinking about permissionless ledgers as a classic example of disruptive innovation and how I think banks could think about permissioned ledgers in the interim.

In what follows, I build up the model below from its constituent parts:

A unified model of permissioned and permissionless ledgers?

Permissionless Ledgers: Censorship Resistance

Let’s be clear: the breakthrough of Bitcoin was to create the closest system yet of “digital cash” – something that you can own outright and transfer to anybody else without permission. Its design flows naturally from that objective:

Bitcoin’s design follows directly from its objectives. Its replicated, shared ledger is designed to enable the existence of a censorship-resistant digital bearer asset

As I argued here, it’s little surprise that bankers and regulators look at it with deep suspicion! However, there’s a good reason why the smart observers aren’t dismissing it: censorship resistance implies an open, neutral platform that could be a driver of permissionless innovation:

Censorship-resistance enables permissionless innovation in digital ownership

So, it’s not a surprise that we’re seeing innovation and experimentation in the fields of value transfer – such as micro-micro payments (nanopayments?) for video content – and in the recording and execution of agreements. This is, almost but not entirely, exclusively being driven by people from outside the traditional financial sector. They’re taking a platform that is, in most meaningful ways, slower and more expensive than today’s financial system and using it for novel purposes.

I think the smart firms are keeping an eye on this because they know how stories like this end:

“Disruptive innovations usually find their first customers at the bottom of the market: as unproved, often unpolished, products, they cannot command a high price. Incumbents are often complacent, slow to recognise the threat that their inferior competitors pose. But as successive refinements improve them to the point that they start to steal customers, they may end up reshaping entire industries” (The Economist)

Permissioned Ledgers: Industry-Level Systems of Record

Notwithstanding the promise – or threat – of permissionless systems, I sense that many financial firms are looking closely at permissioned systems, by which I mean technologies that allow multiple firms to run a private, shared ledger of some sort. What most people fail to ask is: why?! If you don’t have censorship-resistance as your business objective, why are you looking at this space at all?

The answer, I argued, in this piece is that replicated, shared ledgers can also solve a different problem: if you’re in an industry where multiple firms all run similar systems to keep track of records (account balances? derivatives positions? orders?) then you’re probably carrying cost you don’t need: everybody is paying to maintain these duplicated, non-differentiating systems. And, because they’re all slightly different, you need to reconcile them with each other all the time to make sure they agree.

So the argument for applying replicated, shared ledger technology to this problem is that you could mutualise the cost of running and securing a single logical ledger, copied across your firms so you each have your own copy and so aren’t reliant on a powerful central entity for access. So nothing to do with censorship-resistance and nothing to do with cryptocurrencies. The idea, instead, is to move from each firm having its own systems of record to having systems of record at the level of the industry:

Is the promise of permissioned ledger the possibility of industry-level systems of record without a powerful central gatekeeper?

But we can take this thought-process further. Imagine such a platform existed: perhaps a replicated shared ledger that recorded all inter-bank balances or recorded all derivatives positions between firms. What we would effectively have is a transaction processing system for that industry: if we all agree that this shared ledger is authoritative for records (e.g. who owes what to whom) then could we not also agree that this ledger is something to which we could deploy code that describes our agreements? Could this industry-level ledger also host inter-firm business logic? How much cost and complexity might that remove from firms?

Is a common ledger between firms the enabler for a common transaction processing platform for an industry?

And this is where, I think, the two worlds – those of permissioned and permissionless ledgers – come back together:

Unifying the worlds of permissionless and permissioned ledgers

In the permissionless world, some of the most interesting developments are happening at the level of transaction scripting and smart contracts. The Ethereum project is the most obvious example, of course, but even projects like Streamium are showing how Bitcoin features can be used to create interaction models that simply aren’t possible on today’s financial platforms.

Similarly, and as I argued above, the driver of innovation on permissioned ledgers might be the migration of inter-firm business logic from individual firms to a shared ledger between firms: think of code that represents an agreement between two firms, that executes “on” a ledger, which can take custody of assets on that ledger and execute in response to external events: if both firms have signed it off in advance, suddenly they don’t need all the cost and expense of their own systems. I wrote about this idea in my piece on smart contracts.

So we see that the two worlds of replicated, shard ledgers – permissioned and permissionless – might actually be leading us to the same place: a world where business logic for money – automated fiduciary code, if you like – is deployed to a shared ledger and run autonomously.

Perhaps the permissioned and permissionless worlds aren’t as different as they seem?

Posted by

gendal

Posted on

May 12, 2015

Posted under

Bitcoin, blockchain, strategy

Comments

23 Comments

Blockchain is where banks have the most obvious opportunity. But you ignore Bitcoin at your peril

Nasdaq’s recent announcement shows you need a strategy for both

I have argued for some time that the world of “blockchains” is actually two worlds: the permissionless world of “bitcoin-like systems” and the permissioned world of “ripple-like systems”. The reason we so often talk about them together is because they share a common architecture: the “replicated, shared ledger”.

But they solve very different problems. Tim Swanson has written about the permissioned-ledger world and my last post gave an argument for why banks, in particular, should be paying close attention to them.

But this observation can be dangerous if people believe they are building a “blockchain strategy” for their firms when they are actually focusing only on the permissioned world.

As this exchange between Jerry Brito of Coin Center and Michael Casey of the Wall Street Journal shows, Nasdaq’s recent announcement of a blockchain experiment is noteworthy because they are explicitly building on Bitcoin, using a colored coins protocol, not on one of the permissioned/closed ledgers:

https://twitter.com/jerrybrito/status/597543872605069313

I have no inside information into this project. But it should give pause to any who had dismissed bitcoin-based platforms as being irrelevant to finance use-cases.

Forget Bitcoin at your peril?

As I argued in my last post, the world of permissioned ledgers is pretty easy to think about: if you’re in a market where multiple firms in the industry are all building and maintaining undifferentiated systems that do pretty much the same thing – and they have to be reconciled with each other – then it can make sense to replace them with a single system that you all share. But if you’re concerned about having a single central operator then these new blockchain technologies give you an option that didn’t previously exist: you can implement the common infrastructure on a replicated, shared platform that you all help secure/maintain and so mutualise the effort of maintenance rather than delegating it to a separate entity.

But, all too often, the analysis starts and ends there and disregards the “bitcoin-like” world. To see why this could be dangerous, we need to go back to the beginning.

The first nine words of the abstract to the Bitcoin whitepaper tell you everything you need to know to understand its architecture:

Everything you need to know to understand Bitcoin

“A purely peer-to-peer version of electronic cash”

Those nine words seem innocuous but they have profound implications and explain why so many people still steer quite clear of it. The key is “electronic cash”. What can you do with cash that you’d need to emulate in an electronic version?

First, cash is a bearer asset. The only way somebody can take away the money in my pocket is by confiscating it from me. Nobody in a central bank can “delete” my cash whilst leaving everybody else’s untouched.
Secondly, cash is a peer-to-peer instrument: I can pay you directly. There are no third parties we need to rely on, assuming we’re physically co-located

There’s a phrase for this set of requirements: censorship resistance. A true system of digital cash can only work if it is censorship resistant. And Bitcoin’s architecture does a pretty good job of achieving this through a very novel architecture. I sketch out some of the details for interested readers at the end of this article.

There’s just one tiny problem…

Censorship resistance is not an objective that is shared by most governments, regulators, banks or most individuals! No wonder there is so much controversy around the system. Perhaps it’s just easier for respectable firms to steer well clear.

And it gets worse when one observes that Bitcoin is worse than existing digital money in pretty much every significant way! It’s slower, it’s more expensive to operate, its value jumps all over the place and it’s really hard for consumers to use safely. So ignoring it is perfectly understandable.

But it could also be a mistake.

Permissionless Innovation

Because it turns out that censorship-resistance implies an even more interesting property: permissionless innovation.

“Permissionless innovation”—the general freedom to experiment with new technologies and business models—has been the secret sauce that fueled the success of the Internet and the digital economy

Think back to the design goal for the bitcoin system: electronic cash. And how that implied a need for a censorship-resistant bearer asset. These scary properties from a regulatory and banking perspective imply some very interesting properties from a technical perspective: this is the world’s first asset that can be held by anybody or anything and transferred to anybody or anything without needing permission.

Why could that be interesting? Let me sketch three simple scenarios:

The Internet of Things

How do you do KYC on a fridge? Do you really want your washing machine having your credit card details on file? Perhaps the future of machine-to-machine payments is one where the machines hold their own assets on an open system. Sure: you could build a permissioned payments system for device-to-device payments but the simplicity and open-access nature of Bitcoin could mean that it’s just easier to do it that way.

Firms for whom payments are a secondary concern

We often make the mistake of viewing this space through the eyes of incumbents. It can be useful to put ourselves in the shoes of others. For example, imagine you’re building a business for which getting a bank account and payment processing services would be difficult. Maybe you plan to operate in tens of countries. Or perhaps payments are a secondary concern for one of your use-cases… you just need a quick and easy way to make and receive payments. Sure… you could go through the process of getting a merchant account, signing up with a payment processor, proving compliance with various security standards. Or you could just use something with no barrier to adoption: bitcoin may have lots of problems but at least you can be up and running in seconds.

Second-order use-cases

Perhaps the most interesting future scenario is one where bitcoin isn’t used for payments at all. Instead, the security and censorship-resistance of its platform is seen as having value in and of itself – perhaps for notary services in the first instance – recording facts about the outside world – and so Bitcoin becomes nothing more than the token you need to own in order to purchase the services of the network. It becomes an app-coin, if you like.

Why we need to keep an eye on the Bitcoin world

I accept that none of these use-cases is particularly compelling as I write this piece. There are lots of great counterarguments for all of them. But that’s partly the point: if any of these were obvious, nobody would be dismissing it.

And this is why I find the Nasdaq example so interesting. Using the inherent security and open-access of the Bitcoin system to “carry” representations of real-world assets – “colored coins” – is an old idea*. And it also fits into my “second-order use case” category above.

Now, Tim Swanson and others have written convincingly about many theoretical issues with the idea but we now have a brand-name firm experimenting for real and we’ll hopefully all learn from the exercise in time.

So, sure: bitcoin raises all kinds of conceptual, legal, technical and philosophical questions. But it would only take one of these scenarios to drive some adoption and, very quickly, bitcoin might cease to be a sideshow. And, given that its core design goal of censorship-resistant digital cash has such disruptive potential – good and bad, this possibility alone is reason to keep an eye on it. Dismissing it entirely could be a big mistake.

Coda: How to build a system of digital cash

Note: you don’t need to read this section to understand the main argument of this piece.

Recall the implications of a true digital cash system: censorship resistance. This drives some very strong implications for anybody trying to design such a system:

First, you simply can’t have the concept of an issuer in such a system: the issuer could selectively choose to honour only certain claims.

So, if you can’t have an issuer of the currency on such a platform, it will have to be native to the platform. Hence Bitcoin as the currency unit and the interminable debates about why it has value and what that value should be, if anything.

If you want true electronic cash, there can’t be an issuer. So the asset has to be native to the platform

Secondly, you can’t have an identifiable operator or processor for such a system, either: they could choose to block certain transactions and their central database would be an obvious target for those seeking to exert control. So this means you need to have lots of actors providing the processing services and they need to be able to join and leave. And they probably also all need their own copies of the ledger – we can’t have a single central one, after all:

If you want true electronic cash, its ledger will have to be massively replicated and you’ll need a large pool of “processors”

Thirdly, you’ll need to pay the processors. You obviously can’t pay them with “real” money (since the issuer of that money could simply refuse to allow payments to be made to processors who refuse to co-operate with them). So you’ll need to pay the processors with the platform’s own asset:

If you want true electronic cash, the processors will need to be paid in the currency of that platform.

The breakthrough of bitcoin was figuring out how to put these building blocks together: how to ensure sufficient scarcity of the currency unit? How to keep the multiple ledgers synchronized? How to ensure the processors’ incentives are aligned with those of the users of the system? And so on.

There’s more than one way to talk about it

Of course, this isn’t the only way to think about the system. If you’re still interested, here’s my attempt to explain how it works by imagining how you could invent digital cash using an email system.

*Disclosure: I am an adviser to a colored coins firm (ChromaWay) in a personal capacity, albeit one that uses a different architecture to the one apparently being explored by Nasdaq

Posted by

gendal

Posted on

March 30, 2015

Posted under

Bitcoin, Ripple, smart contracts

Comments

19 Comments

Bitcoin as a Smart Contract Platform

Distributed Ledger Platforms may be Getting All the Hype but the architecture of Bitcoin is more sophisticated than many people realise

I was a guest of the Financial Services Club Scotland last week. I presented an update on the world of cryptocurrencies to an engaged and well-informed audience in the library of the Royal College of Physicians.

I reprised my current theme that the world of “blockchains” is really two distinct worlds – the world of Ripple-like ledgers and the world of Bitcoin-like systems – that happen to be united by a common architecture, the Replicated, Shared Ledger. This unifying concept is based on the idea that each participant has their own copy of the entire ledger – and they trust the “system” – whatever system that is – to ensure their copy is kept in sync with everybody else’s. The differences are about what the ledger records and how it is secured.

Bitcoin-like and Ripple-like systems

Broadly speaking, Ripple-like systems are focused on the representation of “off-system” assets and are secured by identifiable entities. Systems like Ripple, Hyperledger and Eris are broadly in this world, I think. The security model of these systems is based on knowing who the actors are: if somebody misbehaves, we can punish them because we know who they are!

Bitcoin-like systems are more focused on “on-system” assets and are secured by an anonymous pool of actors. Bitcoin and Ethereum are broadly in this space, I think. The security model here is based more on game-theoretic analyses of incentive structures: the goal is to make it overwhelmingly in the actors’ financial interests to do the “right” thing.

There is, of course, some ambiguity since all platforms have some notion of “smart contracts” – or otherwise recording real-world agreements, as well as asset ownership. But this makes intuitive sense. If your platform is concerned with real-world assets and agreements then you necessarily need some concept of identity (who are the issuers?). And if you’re reliant on the performance of real-world actors, why not also rely on them for the overall system security? Likewise, if the whole purpose of your platform is to create and manage a new asset that can be controlled/subverted by nobody, then giving identifiable entities the power to control your security would seem to defeat the point!

Different design goals, different implementations. And the value of such systems to banks, corporations or individuals is, ultimately, an empirical question. I imagine 2015 will be the year where we discover many of the answers.

Incrementalism versus “Disruption”

But I went further in my talk. I observed that these two worlds also differ in one other respect: the Bitcoin-like systems could be disruptive to existing institutions if they gained widespread adoption, whereas Ripple-like systems seem, to me, to be far more closely aligned to how things work today and are, perhaps, a source of incremental innovation.

If this observation is correct, then firms looking at this space probably need to assess the technologies through different lenses. The question for banks for Ripple-like systems is: “how could we use this to reduce cost or improve our operations” whereas the question for Bitcoin-like systems is: “how would we respond if this technology gained widespread adoption?”

And to answer the last question, one must be sure to really understand what the system under analysis really is!

Bitcoin as a currency might be to miss the point

For me, it is a mistake to think about Bitcoin solely as a currency. Because the Bitcoin currency system is a masterclass in mirage: underneath the hood, it’s a fascinating smart contract platform.

Or, as I said at the Financial Services Club, every time you make a Bitcoin payment, you’re actually asking over 6000 computers around the world to run a small computer program for you… and your only task is to make sure that the computer program returns “TRUE”. Within the Bitcoin community, this is well-known, of course. Indeed, the work done by Mike Hearn and others to document the platform’s capabilities has been around for years. But I find most people in the broader debate are unaware that the platform is pretty much built on this capability – it’s not an add-on.

Bitcoin is a smart contract platform

I wrote a piece last year offering an intuition for how Bitcoin works, in terms of land. My point was that the fundamental building block of the system is the “unspent transaction output”, or UTXO. The UTXO is what you get when somebody “pays” you some Bitcoin. The “output” of their transaction is the money they paid to you. And whilst it sits in your “wallet”, it is, obviously, unspent. Hence “unspent transaction output”.

So you can think of the current state of the Bitcoin system as being a huge pool of UTXOs: all the payments that have been received by Bitcoin users that they have not yet spent:

Every payment that has not itself been spent is modeled in the Bitcoin system as an “unspent transaction output”. In general, each UTXO can only be spent by the owner of the “address” to which it was sent (not always, and this is the point; see later). And each UTXO has an identifier (the transaction it appeared in and its position in the list of outputs of that transaction) and a value: how many Bitcoins are represented by that UTXO.

But what people often miss is that these UTXOs are actually tiny little computer programs that live on the ledger, control access to bitcoins and run in response to specific incoming events. Smart Contracts, if you will. And the only way you get to spend the money controlled by that contract is if you can provide some input data that allows every node on the system to execute the program and check that it returns “TRUE”

If you can make the program return “TRUE”, you get to say what happens to the funds. If you can’t, then you don’t.

So, when you want to spend your money, here’s what you do:

Your wallet software writes a little computer program for you and then sends it into the bitcoin network. It effectively says to the network: “Please run this little program I’ve just given you. Then please find a program (“smart contract”?) on the platform with this ID for me. When you’ve done that, feed the output from my program into program you just located”. So this is a two step process: you provide your own little program… and the output of that is fed to the UTXO program that you want to spend.

The way you spend money in Bitcoin is to ask the platform to run a small computer program that you provide and feed the output of that program to the “smart contract” that is storing the funds you want to spend. If you can make this second program run successfully, you get to spend the money. In Bitcoin terminology, the program you provide is “scriptSig” and the UTXO program is “scriptPubKey”. Your goal is to provide a “scriptSig” whose output can be fed into “scriptPubKey” to make it return “TRUE”

So what are these little programs? In the common case, they’re really simple. The “UTXO program” simply says: “provide me with a digital signature that proves you own the key associated with the following Bitcoin address (and please also prove that you know the public key that corresponds to the bitcoin address)”. That’s why it’s called the “scriptPubKey”.

And the program you provide is just a way to ensure the bitcoin system sends this proof into the scriptPubKey program in the right way. It’s a way of providing a digital signature. Hence it’s called the “scriptSig”

If you don’t know the private key then you can’t generate the right signature and so you can’t create the input necessary to get the smart contract (scriptPubKey) to run successfully and you don’t get to spend the funds. So this, seemingly complex model, is just a way to ensure that the only person who can spend money at address 1abcde… is the person who knows the private key… exactly as we would want.

Why is it this complex?

But notice how powerful this is… because the other thing you do is tell the system to replace the existing scriptPubKey program with one or more new programs. And this is how your payment is modelled in the system. You pay somebody by creating a new program (a new scriptPubKey) that only they will be able to execute successfully. In this way, you can pay different people or send change back to yourself. The program that only you can run is replaced with ones that only the payees can run. And, in this way, the value has been passed from you to them.

So the result is that the original program living on the ledger is replaced by one or more new programs. In the usual case, one or more of these new ones will be associated with somebody else’s bitcoin address so only they will be able to control it. You have, in effect, paid them that money since the funds are now under their control

Paying somebody in Bitcoin is the same as replacing the program you control with ones they control. In this diagram, the funds you controlled have now been split between two new recipients. Only they can spend those funds.

Smart Contracts?

So what does this have to do with smart contracts? The key is that the model I outlined above is quite generic. The programming language is (just about) powerful enough to implement some interesting business logic that goes beyond “Richard paying money to Bob”. For example, you can write a program that will only return “TRUE” if you provide proof that you know the private key to multiple bitcoin addresses. This is a way to model “a majority of Board Directors must jointly sign before these funds can be spent”, perhaps. The Bitcoin “contracts” wiki page goes into far more depth.

However, the reality is that the capabilities of the platform are actually quite constrained – and I think this explains a lot of the interest in other platforms, such as Ethereum. However, it should be noted that Gavin Andresen has argued that Bitcoin’s limitations need not be a constraint.

So what?

Some might argue that it’s not necessary to think about Bitcoin in this way. But I think that would be a mistake. Because, while lots of people are getting excited about the potential of smart contracts for business, we’ve had a sophisticated smart contract platform running quite successfully for over half a decade, in the form of the Bitcoin network.

Sure – it’s very limited (that’s why systems like Ethereum are getting built). But it might be a mistake to bet that it won’t evolve.

Ultimately, my point is this: even if there’s a low probability of success for a potentially disruptive system, it surely makes sense to understand everything possible about what that system can actually do…

[Disclosure – I provide advice to Hyperledger in a personal capacity.]

[Update – 2015-03-30 Typos and replaced first diagram… I accidentally included an older version that used random IDs for UTXOs that looked like bitcoin addresses, which was very confusing…]

Posted by

gendal

Posted on

January 15, 2015

Posted under

Bitcoin, consensus, ledgers

Comments

29 Comments

Cost? Trust? Something else? What’s the killer-app for Block Chain Technology?

Could decentralized ledgers change the face of accounting?

When I speak to people about decentralised ledgers, some of them are interested in the “distributed trust” aspects of the technology. But, more often, they bring up the question of cost.

This confused me at first. Think back to where this all started: with Bitcoin. Bitcoin is deliberately less efficient than a centralized ledger! Its design adds really difficult engineering constraints to what we already had. How could this technology possibly be cheaper than what we already have?

And yet the claims keep coming. So perhaps this “cost” claim deserves closer consideration. Perhaps there are some scenarios where the “cost” camp might be right?

Ledgers

So much comment in this space talks about “distributed ledgers” or “decentralized ledgers”. But there is very little reflection on what we actually mean by “ledger”.

Investopedia has a good definition of a General Ledger:

A company’s main accounting records. A general ledger is a complete record of financial transactions over the life of a company. The ledger holds account information that is needed to prepare financial statements, and includes accounts for assets, liabilities, owners’ equity, revenues and expenses.

There are some key points here: “complete record of financial transactions”… “information that is needed to prepare financial statements”. I find this a useful definition because it captures two insights that will become important.

first, we use ledgers to record facts… things that the company has done, transactions it has entered in to.
second, the ledger is not an end-product; rather, it’s something from which we prepare other documents – our balance sheet, for example.

A worked example

So let’s work through an example of a balance sheet to test the “cost” argument.

In what follows, I’ll work through a really simple and not-representative example that constructs a balance sheet for a small firm – and asks if there are any opportunities to apply decentralized consensus technology to the problem. (And, as will become painfully clear, I’m not an accountant…)

The world’s smallest and most naïve investment bank…

Imagine you had a fetish for being regulated and decided to start your own TINY investment bank. You persuaded your friends and family to invest £1m and opened the company. You haven’t started trading yet so your accounts are really simple: you have put the £1m you raised in the bank (let’s say Barclays) and, since your friends and family own the firm, you also have £1m of equity – which represents their ownership of the firm. Let’s call it RichardCo.

Hang On – What’s a Balance Sheet?

In my mental model, a Balance Sheet is the financial statement you use as a snapshot of the firm’s financial position at a point in time:

What are all the things you owned at that point (your assets)?
And what are all the things you owe (your liabilities?).
If the difference is positive, great: this is your shareholders’ equity in the business. If it’s negative, it’s game over: you’re insolvent.

So the “balance sheet” for RichardCo on day one might look like this:

RichardCo’s simple balance sheet. There’s £1m in the bank and you record your shareholders’ funds on the liability side of the balance sheet. The “scroll” is the ledger.

By convention, we put the assets (the things you own) on the left and the liabilities (the things you owe) on the right. And we’ve captured a couple of likely entries from various ledgers that explain where the entries on the balance sheet came from.

Notice how we put the shareholders’ funds (the equity) on the “liabilities” side of the balance sheet. This is because the shareholders’ funds can be thought of as a “residual claim” on the company. If you shut it down (or were shut down), you’d have to sell the assets, use the proceeds to pay off everybody you owed money to and, whatever was left, would be the shareholders’. You’d be liable to pay it to them. So we think of the equity as a liability.

Now, like I say, we haven’t done any business yet. But, already, there’s some complexity here

Think about that £1m in cash. It appears on your balance sheet as an asset and you’ll have a record somewhere recording its receipt from your shareholders and another recording the fact that you paid it into the bank. (Actually, you’ll be using double-entry book-keeping and so you will have four entries in the ledger but let’s leave that to one side for now)

Now think about it from the bank’s perspective. They will also have a record. After all, they took it in as a deposit. So it will also appear on their balance sheet – but this time as a liability. They owe it to you.

So there are multiple ledgers in two different organisations all recording the same pieces of information and two balance sheets that reflect the position:

Your balance sheet, recording the claim against Barclays: an asset
Barclays’ balance sheet, recording their obligation to you: a liability

Your £1m asset in the bank also appears on the bank’s balance sheet, as a liability.

Great – this is as it should be and it makes it possible for us to keep an eye on things. When it’s time to get your accounts audited, the auditor doesn’t just have to trust your ledgers. They can phone up the bank and get them to verify that their recording of the position matches yours. The fact you know this can happen acts as a disincentive to cheat in the first place.

If only banks really were this simple…

But, in reality, it’s far more complex than this.

In reality, banks aren’t funded primarily by equity… they also have a HUGE amount of debt…

So let’s imagine you have gone to some pension funds and borrowed £2m – you want to be prudent for now.

Youou decide to build out your broker-dealer arm first so you use the money you borrowed to buy some shares for inventory: £2m of IBM stock. That gets you about 20,000 shares, which you deposit at a custodian bank for safekeeping.

Let’s also imagine that you enter into some interest rate swaps with some other banks. Perhaps LCH.Clearnet, acts as central counterparty for all these trades. And, brilliant news! Your derivatives positions have moved in your favour and it looks like you’re up £1m on them!

Great. So your balance sheet now looks like this.

Your balance sheet after borrowing £2m, entering into some derivatives contracts that move in your favour (£1m mark-to-market – MTM) and buying some IBM shares. Notice how Shareholders’ Funds (equity) has increased by £1m as your assets (the money owed to you by LCH) have increased in value, whilst your debt has stayed the same.

Now think about all the book-keeping at all the other firms

For every position on your ledgers that goes into creating this balance sheet, at least one other entity will also have a ledger that records the same position (from their perspective).

So you might end up with a picture like this:

Your (still very simple!) balance sheet will be reflected on ledgers and balance sheets all across the financial system.

And this picture isn’t the full story. Remember we said the clearing house stepped in and became your counterparty? So the other participants will, in turn, have their own ledgers on the other side of the clearing house. And your shareholders presumably have their own records. And so on.

Making sure all these ledgers are kept in sync: reconciliation

One of the many important control functions in a bank is to check regularly that all these ledgers line up – that your counterparties agree with you on what it is that each of you own or owe to each other.

But, interestingly, you only really need to agree your positions – not the valuations. You could, quite legitimately, come to different conclusions about the value of some positions. For example, let’s imagine that the pension fund thinks there’s a chance you’ll default on your loan. They will still have a record that you borrowed £2m but they may only value the position on their balance sheet as a £1.9m asset.

This is an interesting subtlety: the fact, as shown on the ledger, is that you owe £2m but the pension fund’s balance sheet may reflect their opinion that they’ll likely only recover £1.9m

Similarly, the fact of your derivatives positions is recorded on your (and LCH’s) ledgers. And you’ve probably agreed to pay (or receive) whatever cashflows their systems calculate. But how you value your overall position on the balance sheet could depend on a whole other set of factors.

So perhaps the picture actually looks like the one below: the “facts” that we need to reconcile between firms are those contained on the underlying ledgers, not the subjective valuations on the balance sheets:

In principle, we need to reconcile our ledgers to keep everybody accurate and honest. But it’s perfectly OK for the subjective valuations of some of the positions (as reflected on the balance sheets) to be different – such as with the pension fund here.

So, to simplify hugely, we could say that our problem is one of keeping all these disparate ledgers in sync:

The same picture as before but with the other firms’ balance sheets removed for clarity. Our problem is to make sure these ledgers always agree with each other when they record information about the same transactions.

So we see in the picture above that the facts that underpin my view of the world need occasionally to be checked against at least four other ledgers in other organisations and, in reality, many more.

Enter Decentralised Ledgers

So now let’s turn attention back to the world of decentralized consensus.

I said earlier that it’s hard to argue a decentralised ledger system like Bitcoin that replicates ledger data thousands of times can be more efficient. But perhaps it (or something like it) can.

Imagine we’re living five or ten years in the future. Perhaps we have a securities block chain that records ownership of all securities in the world. Perhaps we have a derivatives smart contract platform that records (and enforces?) all derivatives contracts? Maybe, even, there will be a single, universal platform of this sort.

If so, perhaps all participants would have a full copy of this ledger. And so now maybe we can redraw the picture.

A possible future: all firms record their external obligations and claims on a single shared, massively replicated ledger. Would this reduce (remove?) the need for systems duplication and reconciliation?

Sure – everybody still has a copy of the data locally… but the consensus system ensures that we know the local copy is the same as the copy everywhere else because it is the shared consensus system that is maintaining the ledger. And so we know we’re producing our financial statements using the same facts as all the other participants in the industry.

Does this mean we no longer need audit? No longer need reconciliations? Obviously not, but perhaps this approach is what is driving some of the interest in this space?

But notice: this is just a way of ensuring we agree on the facts: who owns what? Who has agreed to what? We can still run our own valuation algorithms over the top and we could even forward the results to the regulator (who could also, of course, have a copy of the ledger) so they can identify situations where two parties have very different valuations for the same position, which is probably a sign of trouble.

Of course, this is a very simplified example and the real-world is considerably more complex. In particular, some really difficult problems stand in the way of making this a reality:

Scale – think about how many transactions would be recorded
Security – imagine what would happen if somebody managed to subvert the ledger. This also has implications for who controls it, runs it and is allowed to connect to it. Bitcoin’s pseudonymous consensus system is unlikely to be appropriate here?
Privacy – do you really want everybody being able to see all your positions?
… and so on.

So I’m really not saying this is how things will pan out but I think it’s a useful thought experiment: it shows a potential use for replicated ledgers that might have utility but which doesn’t depend on being “trust-free” or “censorship-resistant”.

Perhaps this is what some of the other commentators in this space have in mind?

Posted by

gendal

Posted on

December 19, 2014

Posted under

Bitcoin, consensus, ledgers

Comments

74 Comments

A simple model to make sense of the proliferation of distributed ledger, smart contract and cryptocurrency projects

Just when I think I understand the cryptocurrency/block chain space, I realize I didn’t understand anything at all

Four recent events have made me realize that I don’t understand this space anywhere near as well as I thought I did. But that’s good: it means I’ve been forced to come up with a new mental model to explain to myself how all these projects relate to each other.

TL;DR: the two questions to ask about a “fiduciary code” requirement are: who do I need to trust and what am I trusting them about?

A simple model to capture the essential differences between some consensus platforms

The rest of this article describes the four events that influenced me to draw it.

Event 1: Nick Szabo’s “The Dawn of Trustworthy Computing” Article

In his recent article, Nick Szabo introduces two really helpful terms to explain what makes systems like Bitcoin particularly noteworthy.

First, he talks about “block chain computers”. He defines these as the combination of the Bitcoin consensus protocol and strong cryptography to create the unforgeable chain of evidence for all data stored in the block chain data structure. I think this formulation is useful because it shines a bright light on an obvious, but often overlooked fact: a “block chain” is just a data structure, utterly useless on its own. What makes the Bitcoin blockchain remarkable is the network of computers – and protocol they follow – that makes it so hard for any single actor, no matter how determined, to subvert it.

Secondly, he talks about “fiduciary code”: the code in an application that needs to be the most reliable and secure. For example, in a banking application, this is likely to be the core ledger: who owns what. He points out that a secure block chain computer is an extremely expensive piece of kit: you should only use it to secure that information that really needs it.

Event 2: Albert Wenger’s “Bitcoin: Clarifying the Foundational Innovation of the Blockchain” Article.

In this piece, Albert Wenger makes a really obvious-in-hindsight point: Bitcoin-like block chains are organizationally-decentralised – no one organization can control it but the entire point of the system is to build and maintain a logically-centralised outcome: a single copy of the ledger, which everybody agrees is the true single copy.

ArthurB uses the term “decentralized mutable singleton” to capture the same idea, I think.

Repeat after me: if you don't need concurrent access to a decentralized, mutable, singleton, you don't need a #blockchain.

— Arthur B. 🌮 (@ArthurB) December 17, 2014

And he echoes one of Szabo’s implicit points: a “block chain” is not something of value in and of itself. This insight is also important because it edges us further away from the idea that “decentralization” is some sort of end-goal or absolute target. I made a similar point in this piece on the “unbundling of trust” but Albert and Arthur have captured the key point far more succinctly.

Event 3: The Eris Launch

On Wednesday this week, Eris Industries held the launch event for their new platform. Tim Swanson has done a good job summarizing the Eris concepts. (Disclosure: I was invited to, and attended, the launch).

I’ll admit I still don’t fully understand it. But the general picture that’s forming for me is of a platform that allows you to build and maintain one of these “decentralized mutable singletons” but to specify precisely who is allowed to update it and under what conditions.

In essence: take the idea of a shared common state (~~Albert’s~~ Arthur’s “mutable singleton”) but relax the constraint that the maintenance of it necessarily happens in a fully public, adversarial environment, for which something like a proof-of-work system may be required, and allow for the idea that the participants might be known. [EDIT wrong name!]

Fine… but I think the Eris insight is where they go next. They suggest that if you had such a system then you might also be able to distribute the processing of application logic more broadly, too. And I think it’s the application logic they’re most interested in. Their documentation is full of talk of “smart contracts” and it’s perhaps no surprise that their founders are lawyers. In fact, maybe that’s why I don’t understand it as well as I’d like: lawyers just seem to speak differently. Maybe I need a translator.

And to be clear, the part I don’t fully understand just yet is why you need a “block chain” as the underlying data structure in this model, rather than something based on more general-purpose replicated database technology. But this may turn out just to be an implementation detail: so let’s see how they get on over time. There seems to be a lot of content, reflective of a lot of thought, on the various Eris sites.

Event 4: I looked at HyperLedger in more detail

I had reason to look at HyperLedger this week and, combined with my study of Eris, it was this event that finally convinced me that my mental model of this space was far too simplistic.

Hyperledger calls itself an “open-source, decentralized protocol for the recording and transferring anything of value”. This is a bit like how I might have described Colored Coins or Ripple to people in the past.

But what makes Hyperledger different is that they allow the creation of multiple ledgers (one per asset per issuer) and each ledger can be configured to have different consensus rules – you don’t have to make the assumption of an adversarial open public environment… so some similar assumptions to Eris here, but with a ledger designed to track assets rather than business logic/contracts.

Where is this heading?

So I spent some time this evening trying to piece all of this together in my brain.

I’m pretty sure these projects all sit in Szabo’s “Fiduciary Code” space: they only really have value or make sense if the facts they’re recording are really important!

But they make different assumptions about the threat model they face – and some of these assumptions are very different to the ones against which Bitcoin was designed. And they’re different to the assumptions underpinning some other prominent platforms, such as Ripple, which, through its use of validators and “Unique Node Lists” has a model, whereby you trust a set of known entities who, in turn, trust some other entities, and so on.

In addition, the facts these systems are recording are very different: ownership of a real-world asset on Hyperledger is different to ownership of a bitcoin on the Bitcoin ledger; a ledger-native asset has no counterparty risk, whereas a real-world asset needs an identifiable issuer. And they’re both different to a platform that potentially executes legal contracts.

So I tried to think of dimensions along which you might be able to classify these projects… and I came up with too many.

But it’s almost Christmas and I’m not to be deterred! Is it really too much to ask for a model with just two dimensions, that doesn’t require a 3-D screen to render?! So I kept on going. And, finally, came up with something that looks so trivial, I worry it may be content free. But here it is anyway.

I think the two dimensions that help me think about these projects are:

“Who do I trust to maintain a truthful record?”; and
“What do I need the record to be about”?

Here is the model I came up with. It’s obviously not complete and you could put some projects in multiple boxes… but I think it captures the key distinctions.

Another way to think about the increasingly confusing cryptocurrency/Block Chain space

But this is just a view. I’d really value comments… especially if I’ve missed something really obvious.

[UPDATE 2015-01-08 DISCLOSURE: Since publishing this post, I have become an advisor to HyperLedger, in a personal capacity]

Posted by

gendal

Posted on

December 3, 2014

Posted under

Bitcoin, identity

Comments

24 Comments

Identity and The Blockchain: Key Questions We Need to Solve

What are the architecturally-significant use-cases for identity?

Some of the most interesting uses for cryptocurrency technology in finance are securities processing, supply chain finance and derivatives operations. These are areas where there should be almost total automation but there is, in reality, still large amounts of manual processing, rework, reconciliation, complexity and endless opportunity for confusion and dispute.

To help think about how blockchain technology could play a role, I suggested the “trust bundles” concept as a way to think about which aspects of a given business, such as securities exchange and settlement, could be moved onto a decentralized consensus system – and what benefits might accrue.

However, there’s a big problem that needs to be addressed before many of these opportunities become realistic. That problem is identity. The anonymity (or pseudonymity) of Bitcoin may be great for some use-cases but it doesn’t help a firm accused of paying a “crypto dividend” to a terrorist if they have no way of proving they didn’t!

So let’s imagine we’re living in the future… Smart property technology means that securities can be issued and traded on a blockchain-like system and smart contract technology has allowed us to move all derivatives contracts onto a global platform.

What identity problems would we need to have solved for that future to come true?

Smart Property Issuance

Imagine you’re an investor. You have a Smart Property wallet. Perhaps it contains multiple cryptocurrencies, some bank-issued fiat currencies and your equity portfolio, safely secured with a multi-signature scheme.

You decide you want to add some IBM stock to your portfolio. So you instruct your wallet to place an order on a decentralized equities exchange.

What do you place the order for?

What do you physically type into the user-interface to tell it you want IBM stock and not somebody else’s stock?

It would be nice if you could simply type “IBM”.

But how would that work? We’re in a decentralized world, remember. We’ve “unbundled trust”. So how should the wallet interpret “IBM”? Which asset on the decentralized ledger represents the “real” IBM? A Namecoin-like system doesn’t help if a “cryptosquatter” took the IBM name before the real IBM did.

And, in any case, what do you mean by “IBM”?

Intuitively, you probably mean something like: “The big American IT company based in Armonk, New York that had 2014 revenues of about $100bn and is a component of the Dow”. Or something like that. But how to capture that intuition in a way that a decentralized network can interpret?

And how to distinguish the security you want from something similar (and legitimate) issued by somebody else? And, of course, how to distinguish it from a security issued by a fraudulent third party who is trying really hard to fool you into buying their product?

In a pseudonymous world, how do I distinguish “real” blockchain assets from scams?

One really unimaginative way would be to do what we do today: just decide to trust somebody to do the mapping for you. Tell your wallet that you trust Bloomberg or Markit, say, to maintain a directory and you’re done. This would be an oracle service, in effect.

But this is a new point of centralization. Whoever controls that list can extract a rent and they are a source of risk: what happens if their database gets hacked or a rogue employee changes the records? Maybe having multiple oracles is the way forward.

Alternatively, perhaps we can use the internet X.509 Certificate system as a model. But even that would require some thought: you don’t want your webmaster issuing a $1bn bond!

What does it mean to be an issuer?

But we also need to think about it from the perspective of the issuer and this is altogether more difficult. To keep things interesting, let’s use a currency example this time.

Imagine we’re still in the future and I am a customer of Citi with a $1M balance. I could ask Citi to issue a token on the blockchain representing this balance and send it to my wallet. My balance in my Citi account would be converted into ownership of a token representing $1M USD. (I shouldn’t need to state it but I will: I chose Citi purely as an example. I have no insight into their plans, if any, in this space!)

Richard is a Citi customer. Citi converts Richard’s balance into a “CitiUSD” token on a blockchain and sends it to Richard’s “1RICHRD” address

So I would now be a holder of a 1M CitiUSD token, owned by my “1RICHARD” address. Note that this is essentially what happens when I use a gateway on the Ripple system but let’s assume we’re on a blockchain system for now to keep things consistent.

Aside: imagine if all banks did this… we could have CitiUSD, ChaseUSD, BarclaysGBP all issued on the same platform. Perhaps they’d trade at different prices based on market perception of their credit-worthiness? Prices as a function of CDS spreads perhaps?

Now, Citi would know exactly who I was: I was already a customer, remember, and they needed to know my blockchain address to issue the token to me.

But think about what happens next. I now have full control of this token.

So I could send it to anybody else in the world. And that person would now own a token representing a claim of $1M against Citi. Let’s imagine I bought a house from Charlie and paid using my CitiUSD tokens, sending them to his blockchain address, 1CHRLIE

I “pay” Charlie with my CitiUSD tokens. So Charlie now owns the claim on Citi. But Citi had no part in this transaction…

What would Citi think about this? Who is “1CHRLIE”?? Are they already a customer? If not, how do they know if “1CHRLIE” is a “good guy” or not? Is Citi obliged to pay $1M upon presentation of the token?

More trickily, what happens if the token has passed through the hands of a “bad guy” at some point between issuance and redemption? Sure – the initial owner of the token might be OK – and the person presenting the token some time later for redemption might also be OK. Perhaps we do know that 1CHRLIE is Charlie and that Charlie is a Chase customer and we’ve doubled checked with Chase. But do we need to know who has held the token in the intervening steps?

Do we need to know the identities of everybody who has ever owned a token?

What if one of the intermediate owners was 1TRRST, aka “Terry the Terrorist”?

You can be pretty sure we do need to know something about them. Good luck if you try to tell your regulator that these tokens are “bearer assets” that are morally equivalent to cash!

So, leaving aside the possibility that we just don’t go down this road at all, what are some of the options for making this work?

I think there are two broad options:

Option 1: Ex-Ante Prevention – The Issuing Bank “Co-Signs”

This option is pretty simple. You change the model so that these assets are not bearer assets. Holders of Citi tokens need to get Citi to co-sign any blockchain transactions that move the asset. So Citi gets the chance to vet the recipient and check they’re happy owing them money. You can think of this as “ex ante prevention”. It would work, of course, but it would heavily constrain the usefulness of such a system.

Option 2: Ex-Post Prevention – The Bank Won’t Pay Up Unless You’ve Behaved Yourself

This option is more interesting. You can send the token wherever you like, but if you want to redeem the token for real USD, the bank will ask you to prove that everybody who ever owned it was a “good guy”. If you can’t prove a clean ownership history then the token is worthless; the bank won’t pay up.

Leaving aside the question of what we mean by “good guy” and the natural worry that this could give banks an excuse to renege on their commitments, how might you do it?

First, let’s cover off the obvious option. The obvious option is simply to say: “We’ll only redeem a token if its ownership chain consists only of Citi customers”. Or perhaps you could extend it and say: “We’ll only redeem a token if its ownership chain consists of customers of the following banks”. The latter approach might pave the way for an industry “register” that maps bank identifiers to blockchain addresses. Again, we’re back to centralization and the very real risk of a “balkanization” of the system: you would effectively have “white” addresses and “black” addresses – those that can hold banking-system assets and those that cannot.

If several of my readers are about to explode in outrage, bear with me because this isn’t what I’m proposing…. Happily, there could be another way.

“Identity is the New Money”

I was fortunate last week to attend Consult Hyperion’s “Digital Identity” unconference at Barclays Bank’s “Escalator” venue in East London. Our host, Dave Birch, encouraged the audience to really exert themselves to think deeply about questions of digital identity. It gave me the motivation I needed finally to read his book, “Identity is the New Money”. I recommend it. It’s short, snappily written and made me think.

One of his key themes is that we’re thinking about identity all wrong. Most of the time we think we need to know who somebody is, what we actually need to know is something about them:

A bartender doesn’t need to know your name; they just need proof you’re over 18.
A UK doctor doesn’t need to know what town you were born in to know if you’re entitled to free healthcare.
… and so on

Similarly, and at a very conceptual level(!), what an issuer of USD tokens on a blockchain needs to know is probably something like:

The actor who controls an address is a legal person…
… and this person has a US bank account…
… and somebody has studied this person’s identification documents closely and has no concerns about them…
… and whoever is making these statements about them is trusted by the issuer of the tokens (say Citi)

Now, I say “conceptual”, because AML, KYC and CDD regulators might not see things this way yet but let’s keep going…

What these concepts all have in common is that they have this idea of a “certifier” – somebody or something that:

Is trusted by the issuer
Ties something I have (my face or my blockchain address) to something I am (“over 18”, “a holder of a US bank account”, etc)

If you trust the certifier then you can trust that somebody proving ownership of the face or the address is over 18 and a holder of a US bank account, etc.

What does a bank need in order to be satisfied?

So now let’s return to our currency example. Remember the problem we’re trying to solve: If I am Citi, I want to be sure that anybody who has ever held one of my tokens is somebody I am allowed to transact with.

So how could we achieve this without a centralized database? Well, imagine Charlie is a customer of Chase.

Let’s assume Chase knows who Charlie is and is satisfied that Charlie is a good guy.
So if Charlie can prove to them that he controls a particular blockchain address, they might be willing to issue him with a “certificate”
This certificate might say: “I am Chase. Here’s my proof. I know who is the owner of address 1CHRLIE…. That person is a US Citizen and, as of 3 December 2014 was a retail customer, with a good account history and no warning signs on his account”

And perhaps I could get a certificate from Citi that says they think I’m a “good egg” and one from the UK government confirming I’m a UK citizen:

Could asset issuers use certificates from third parties they trust to satisfy their regulatory and other “client due diligence” requirements?

So now we have something really interesting.

An issuer can set down their conditions when they issue the asset. They could say something like: “I will redeem this asset at par if the redeemer can prove that they and every intermediate owner was a US citizen with a KYCd US bank account. I will accept proof from any FDIC insured bank”.

So if I was considering buying a CitiUSD token from somebody, I no longer care who they are. I just care that they possess one or more certificates that comply with the conditions that were specified in the definition of the asset. My wallet software could even check it automatically for me.

And when somebody wants to redeem the token, they simply return it to Citi, with the chain of certificates and Citi can immediately tell that the token has only been in the hands of people with the attributes it specified. No need to reveal my identity to anybody and no central third parties we need to trust. If somebody does need to figure out the identity, they can get a court order and the certifier will reveal it.

Reality is more complex. In particular, how to stop a black market in certificates? e.g. a “mule” obtains a certificate for a blockchain address and then turns over the certificate and the address’s private key to a bad person. A difficult problem to solve but probably not unsurmountable.

But the underlying principle is absolutely crucial: if we’re moving to a world where trust is unbundled and control is decentralized, we need to rethink identity. Anchoring it in a diverse set of “certifiers”, who attest to the linkage between something I have (a blockchain address? My face?) and something I am (British, Over 18) surely has to be the way forward.

Posted by

gendal

Posted on

November 14, 2014

Posted under

Banking, Bitcoin, exchanges, Payments, Ripple, Securities Servicing

Comments

12 Comments

The “Unbundling of Trust”: how to identify good cryptocurrency opportunities?

Decentralization and centralization are two ends of a continuum. Look for opportunities to disaggregate “bundles of trust” to identify good opportunities in the cryptocurrency space

There are so many potential uses for cryptocurrency technology. But how do you know if any of them are good ideas? Blockchain-mediated financial exchange? I have a good feeling about that one. A bank-sponsored local currency system for small businesses? My sense is that it’s probably a terrible idea. But short of going out and building it, how would you know?

So are there any test you can apply beforehand to figure out if a blockchain is a good technical solution for a given problem? And can you turn a bad idea into a good idea?

It’s a topic that comes up regularly when I present to audiences on Bitcoin and cryptocurrencies. Here are some slides I often use in these discussions. Slide 15 is where I discuss this topic.

Slides I sometimes show when presenting on cryptocurrencies. These represent my views, not IBM’s. But they are Copyright IBM. Please do not reproduce without asking permission first.

For me, the key to deciding if an idea is good enough is the one I’ve summarized on page 15 of the deck: this space is all about decentralization and if your problem isn’t about centralization then this technology may not be for you.

That may sound obvious. But internalizing this point is the key to understanding what a good cryptocurrency use-case looks like. And how to turn a bad one into a good one. Because even if your problem looks centralised, there may be portions that don’t need centralised trust and unbundling those components could be the key to doing something valuable. Here’s what I mean…

Go back to the beginning: what problem was Bitcoin designed to solve?

Bitcoin was invented as an answer to a decades-old question:

How do you come to consensus about some facts with a large group of people when you don’t know each other and some of you are cheating?

In Bitcoin’s case, the “facts” are “who owns what?”

And one answer to that question is, of course: “we all agree to trust somebody (e.g. a bank) and now we don’t need to trust each other”. But the obvious problem is: you have to trust the bank and that’s a potential point of failure. The breakthrough of Bitcoin was in showing us how to answer this question in a way that doesn’t require us to trust any single third parties.

We say the system is “decentralized”, as a shorthand for this concept.

(As an aside, I explained Bitcoin from first principles in this post on how the counter-intuitive genius of Bitcoin is that it works by going slow! For those who want to go even deeper, I share a way to think about the confusing “Unspent Transaction Output” concept in Bitcoin through an analogy of land.)

This is why Bitcoin is often positioned as being a decentralized equivalent to the centralized banking system:

Bitcoin allows us to agree who owns what without having to know each other or trust anybody else. This is the opposite of the traditional system where everybody has to trust their bank

Bitcoin-as-envisaged isn’t what we have

But there’s a problem: Bitcoin-as-envisaged isn’t what we have today. Phenomena such as mining centralization and the use of SPV Wallets mean that Bitcoin isn’t completely decentralized. It’s not currently a problem but one can already see its effects. For example, some miners refuse to mine certain types of transactions. The effect on average confirmation time for these transaction types might be marginal but it exists, nevertheless.

So Bitcoin-today is somewhere in between. It’s not 100% decentralised yet nor is it centralized.

Bitcoin today is neither fully decentralized nor is it centralised

So it seems reasonable to consider that centralization may actually be a continuum rather than an either/or phenomenon:

Are centralization and decentralization actually two ends of a continuum?

This way of thinking can be helpful because it allows us to think about other innovations in this space, such as Smart Property.

Smart Property

I’ve written in the past about a decentralized securities systems being built “hidden in plain sight”. The key idea here is that you can use blockchain platforms (like colored coins or counterparty, etc) to track the ownership and transfer of real-world assets. What distinguishes these platforms from Bitcoin itself is that they have to bridge to the real world: the asset could be a bond with a corporate issuer, being kept safe by a custodian bank, for example. So there are several real-world entities on whom you depend.

I’ve written about how smart property allows these two roles to be merged (the issuing company could do both) but somebody has to do it – let’s just call them issuers.

So this system has points of centralization (the issuers) and points of decentralization (the ownership tracking and exchange). So perhaps it sits somewhere here on the continuum:

Perhaps there is value in different “degrees” of decentralization for different business problems

You can have more than one type of decentralization in a single service

But it’s actually more interesting than that. Because not only do smart property systems sit somewhere on the decentralization continuum, the key point is that different parts of the systems sit in different places:

the ledger, exchange and transfer system use the underlying Bitcoin consensus system – so they’re all pretty decentralized. No need to depend on any trusted third parties.
But you do, of course, have to trust the issuer. That part of the proposition is centralised

So the important thing about smart property systems is that the all-or-nothing “trust bundle” is unbundled: you need to trust a specific issuer but the ledger, exchange and transfer functions are decentralized in their operation.

The unubundling of trust

And I think that’s what gives decentralised consensus systems some of their power: you can now break down products and services into their constituent elements of trust and implement each one with the most appropriate degree of centralization. For smart property, perhaps the picture looks something like this:

Different degrees of decentralization can exist within the same service: trust is being unbundled

So what?

Of course, none of this tells us whether smart property or cryptofinance is a good idea. But it is a way to think about whether a particular service is doing anything particularly novel. Think about it the other way: if somebody proposes a cryptocurrency business idea that doesn’t meaningfully unbundle any trust in an existing service, is it actually doing anything valuable? Likewise, take any real-world centralised service and ask yourself: what are all the things I need to trust for this to work? Which components have to be centralised? Which could be decentralised? Does that lead to lower risk? Lower cost? More opportunities for competition? Reduced friction for consumers? If the answer is “yes” to those questions then you could have an interesting proposition on your hands.

Unbundling trust in payments

A similar analysis works for systems like Ripple. Ripple’s architecture is more distributed than the traditional payments systems but less so than Bitcoin (at least as envisaged) so perhaps we may place it somewhere like this on the scale:

Ripple is another example of a “trust unbundling”

But, just like in the Smart Property example above, in the Ripple system there is a “trust unbundling” going on: the ledger is fairly decentralized in its operation whilst you necessarily need to trust a specific gateway. So it actually looks like this:

Different degrees of decentralization can exist within the same service: trust is being unbundled

To see why this is important, recall how current payment systems work. I wrote a simple explanation of it here. As the article shows, you have to trust a lot of moving actors and the point is that you have to take this as a bundle… it’s all or nothing. You trust all those parts of the system or you can’t achieve your objective. With a Ripple-like system, you only trust the minimal set of actors you have to – namely, the banks who issued liabilities. Everything else can be decentralised to some degree.

Unbundling trust in contract execution

One last example: a similar argument applies to financial contracts. Projects like Ethereum (and Counterparty!) are exploring the decentralized modeling and execution of law. Gavin Andresen has written about how something similar could be achieved on the base Bitcoin platform.

You can think of this in terms of “trust unbundling” too: the decentralized platform ensures the integrity of contract execution and you can use n-of-m oracles to provide reliable external data. You only trust who you have to, to the minimal degree possible.

Using “trust unbundling” to turn bad ideas into good ideas..?

So now we can put this model to the test. Does it help us spot the silly ideas? Even better, does it help us turn the silly ideas into good ideas? [UPDATE 2014-11-15 this section was heavily reworked)

Antonis Polemitis commented on an earlier version of this article:

@gendal I find a good theoretical example to be airline points. today centralized issuer and centralized / clunky clearing/settlement/etc

— Antonis Polemitis (@polemitis) November 14, 2014

Here’s what I think he means:

A better airline miles system?

As Antonis points out, airline miles systems are highly centralised: the airline is the issuer, redeemer, owner of the ledger, setter of the rules and controls everything else too.

So imagine an airline were to announce that their new airmiles programme was to be based on a fork of Bitcoin. Perhaps they would create their own Blockchain, issue the miles on top, secure it themselves and distribute wallets to all their customers. Brilliant… an airline miles programme with all the benefits of Bitcoin!

Really? From a consumer perspective, surely this system would be indistinguishable from a traditional system and what is the argument that says it would be better in any meaningful way?

But take a step back and think about airline miles again and think about the trust bundle. Which parts of the system require you to trust the airline? Issuance and redemption of the miles, for sure. And setting of the scheme rules. But storage, exchange and trade doesn’t need to be done by them.

And perhaps there’s a cost saving for airlines if they offload that work to a decentralised network and a benefit for customers if it gives them additional utility – perhaps new ways of swapping miles between competing programmes to accumulate enough points to book a flight? Some very interesting possibilities emerge if multiple airlines base their systems on the same platform or if third parties can build new services on top of a platform like this.

Suddenly you might have something interesting: an interoperable, multi-provider airline miles storage, transfer and redemption platform. Now it could be a terrible idea – these schemes only work because most miles are never redeemed, after all! But the thought process is important: who are users expected to trust to use your service? And what are they trusting them for? What if a component was decentralised? What new possibilities would that enable? What risk could it mitigate?

Now the real world is more complicated than this. But the key insight remains:

if your cryptocurrency idea requires users to trust only you, you’re missing the point
but if there’s something in the value proposition that can be usefully decentralized or shared with others, you could be on to something